Matemáticas con las manos - Juan S. Barrero

Parábola de seguridad      

PARÁBOLA DE SEGURIDAD DEL TIRO PARABÓLICO

Supongamos un cañón situado a nivel de suelo que dispara un obús con un ángulo de inclinación θ y velocidad inicial de disparo v₀.

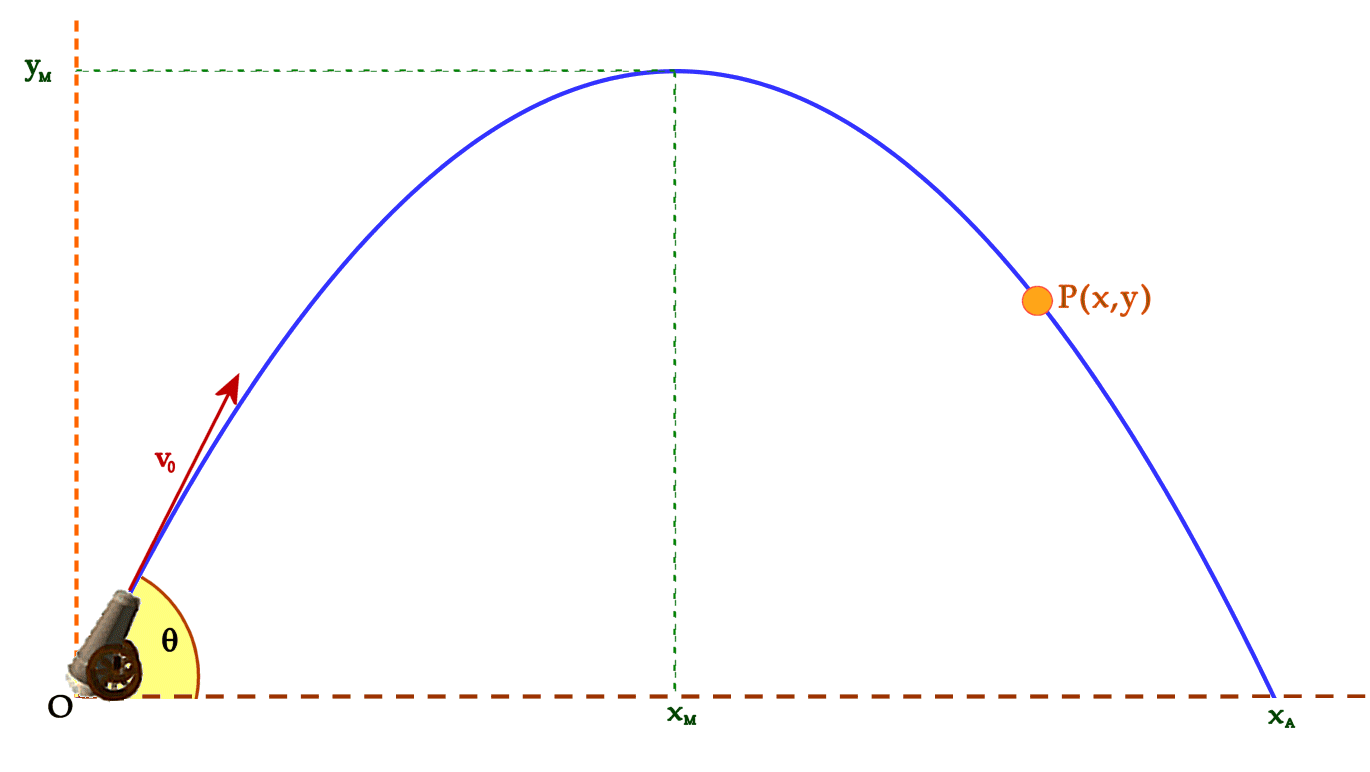
La trayectoria que describe el obús sigue la ecuación:

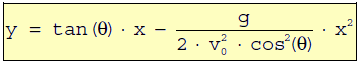
que es una parábola con un máximo en x_M y que corta al eje de abscisas en x₀ = 0 (punto de disparo) y x₁ = x_A (punto de máximo alcance).

Si mantenemos fija la velocidad inicial y vamos efectuando disparos con distintos ángulos, ¿existe alguna línea que determine el límite de seguridad a partir de la cual el cañón nunca nos alcanzará?
Si representamos todas las trayectorias con diferentes ángulos de disparo:

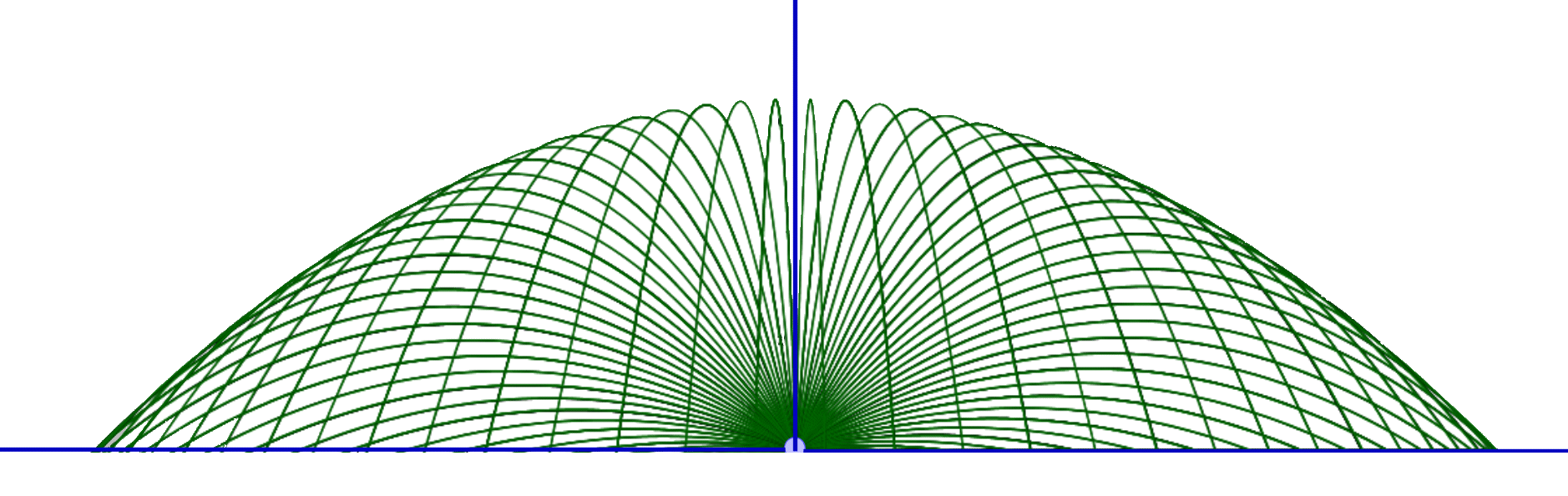
Obviamente sí. Esta curva se llama parábola de seguridad.

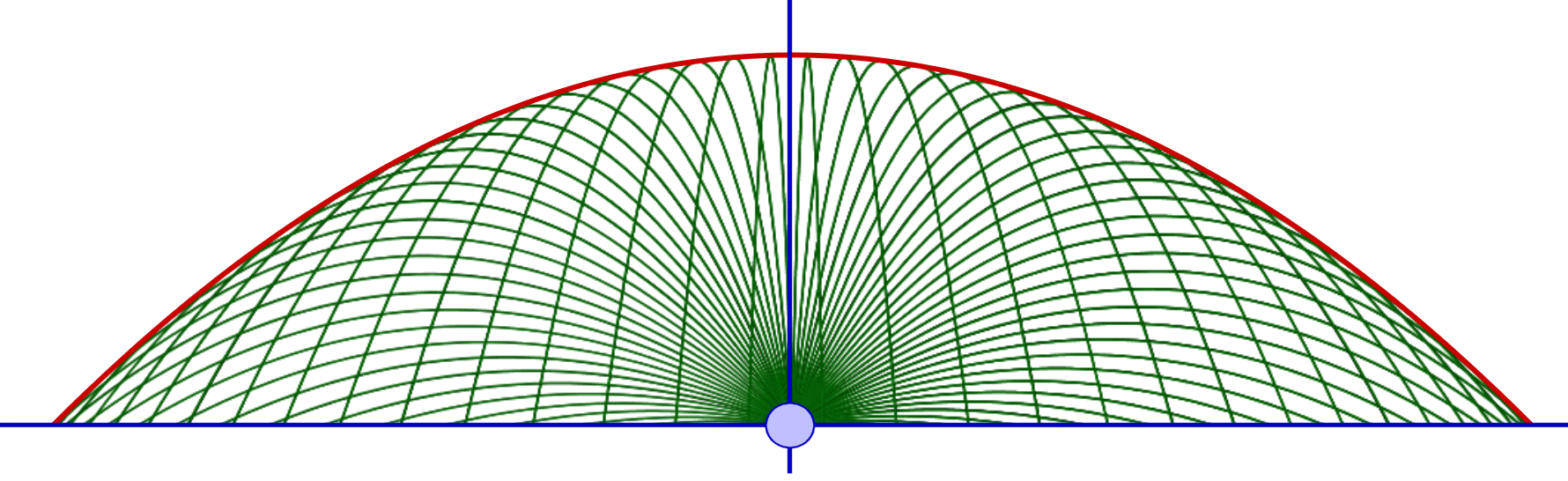
Tiene por ecuación:

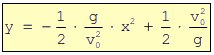
que es la ENVOLVENTE de todas las curvas (trayectorias) que varían con respecto al ángulo de tiro manteniendo constante la velocidad de disparo inicial.